classification and clustering
聚类
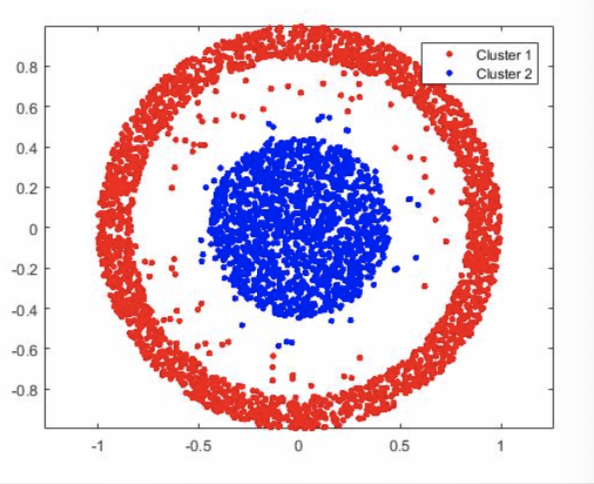
什么是聚类
一类数据点的集合
类内相似性
类间差异性
衡量聚类好坏的标准
最大化类间距离
最小化类内距离
数值闵可夫斯基距离
d(X,Y)=∥X−Y∥p=(∑i=1n∣xi−yi∣p)1pd(X,Y)=\Vert{X-Y}\Vert_p=(\sum_{i=1}^n\vert{x_i-y_i}\vert^p)^{\frac{1}{p}}
d(X,Y)=∥X−Y∥p=(i=1∑n∣xi−yi∣p)p1
L1曼哈顿距离
d(X,Y)=∣X−Y∣d(X,Y)=\vert{X-Y}\vert
d(X,Y)=∣X−Y∣
L2欧几里得距离
d(X,Y)=(x1−y1)2+(x2−y2)2d(X,Y)=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2}
d(X,Y)=(x1−y1)2+(x2−y2)2
切比雪夫距离
d(X,Y)=limp−>∞(∑i=1n∣xi−yi∣p)1p=maxi∣xi−yi∣d(X,Y)=\underset{p->\infty}{lim}(\sum_{i=1}^{n}\vert{x_i-y_i}\vert ...