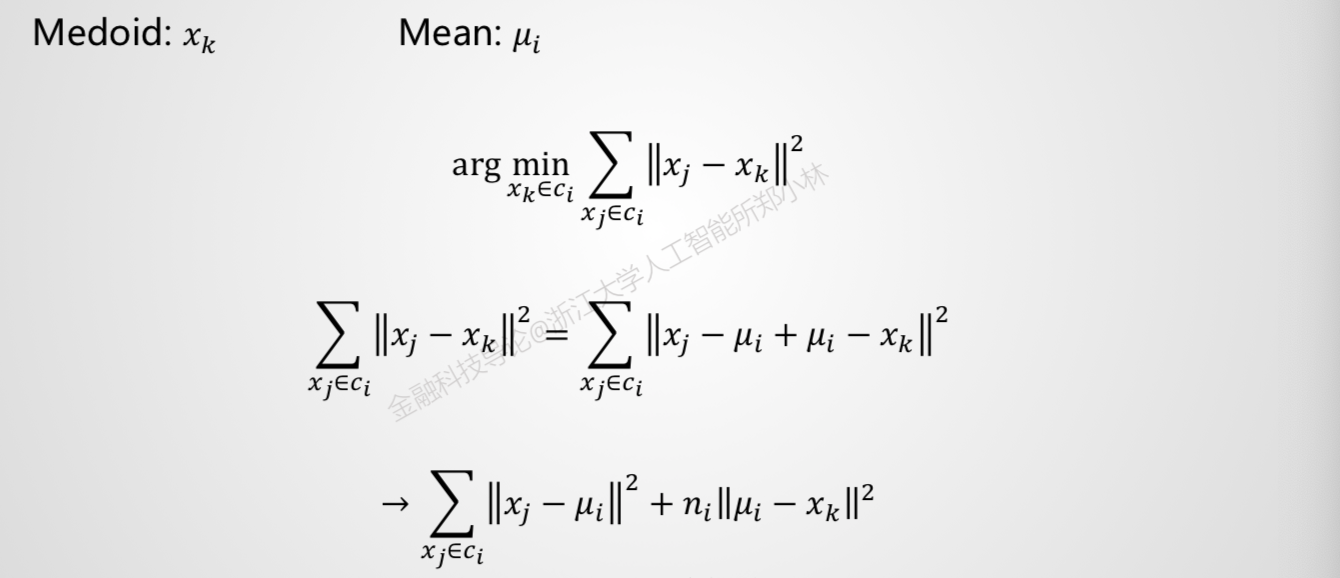聚类
什么是聚类
一类数据点的集合
衡量聚类好坏的标准
数值闵可夫斯基距离
d(X,Y)=∥X−Y∥p=(i=1∑n∣xi−yi∣p)p1
-
L1曼哈顿距离
d(X,Y)=∣X−Y∣
-
L2欧几里得距离
d(X,Y)=(x1−y1)2+(x2−y2)2
-
切比雪夫距离
d(X,Y)=p−>∞lim(i=1∑n∣xi−yi∣p)p1=imax∣xi−yi∣
-
向量-余弦相似度
cos(d1,d2)=∥d1∥⋅∥d2∥d1⋅d2
余弦相似性是通过测量两个向量的夹角的余弦值来度量他们之间的相似性
K-means
已知观测集(x1,x2,...,xn),其中每个观测都是一个d-维实向量,k-平均聚类要把这n个观测划分到k个集合中(k≤n),使得组内平方和(WCSS within-cluster sum of squares)最小。换句话说,它的目标是找到使得下式满足的聚类Si
argsmini=1∑kx∈Si∑∥x−ui∥2
其中μi是Si中所有点的均值
总之:思想是最小化类内距离平方之和
方法
随机选取k个聚类质心点,u1,u2,⋯,uk∈Rn
重复下面过程直到收敛
对每一个样例i,计算其应该属于的类 c(i):=argminj∥x(i)−uj∥2
对每一个类j,重新计算该类的质心 uj:=nj1∑xj∈c(j)xj
pseudocode

特点:
- 简单快速
- 聚类结果容易收到起始点影响
- 聚类结果在向量空间为球状[凸集]
- 聚类结果容易收到噪声[脏数据]影响
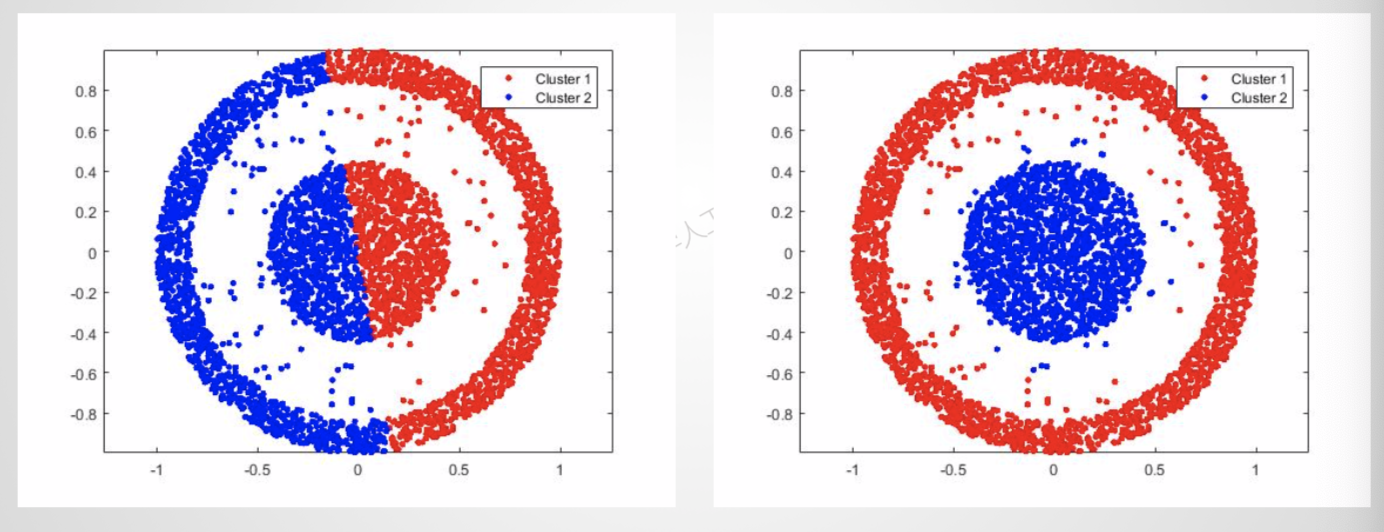
k-means是做不到第二种聚类效果的
K-medoids
Mean:聚类的中心
ui=ni1xj∈ci∑xj
Medoid:聚类的中心数据点[到类内每个数据点到距离之和最小]
算法:
1、把所有数据划分为k个非空子集
2、计算每个子集的中心点[mean]
3、把离中心最近的数据点[medoid]作为该子集的实际中心点
4、把所有数据点重新划分[划分到离该数据点最近的中心点]
5、重复步骤2,直到中心点不发生变化
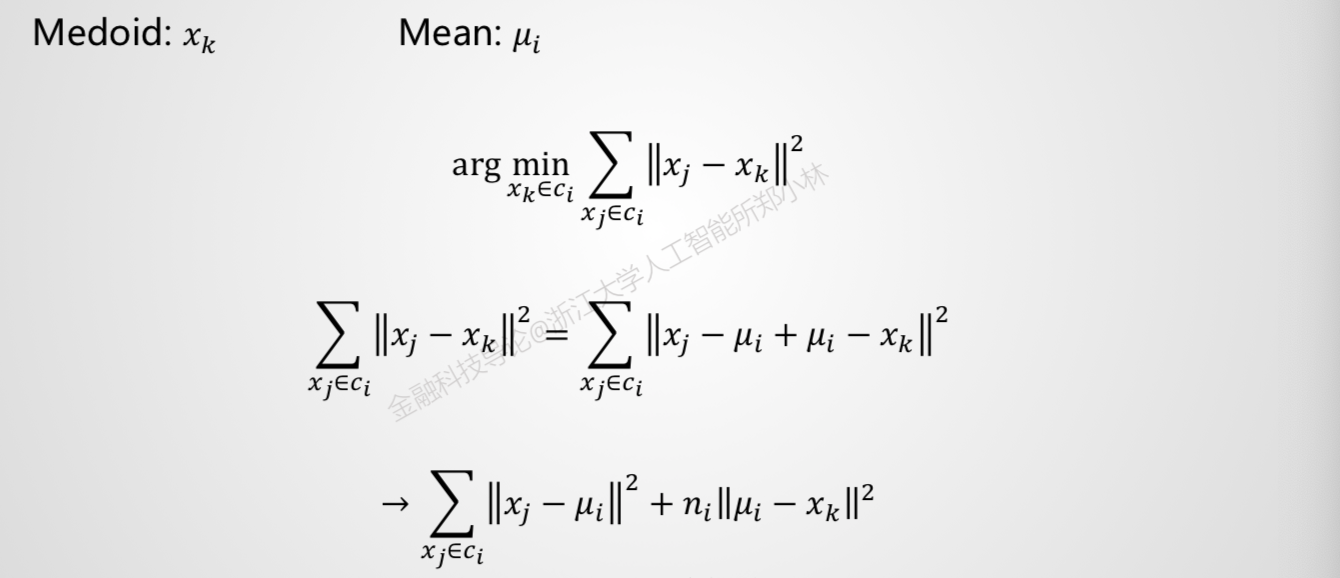
谱聚类
思想:把数据集看作带权无向图,将图切分成多个不相交的子图,使子图内相似度较高,子图间相似度较低
- 找到最小切分mincut(A,B)
cut(A,B)=∑i∈A,j∈Bwij
A与B两类之间相连边的权重
- 最大化类内连接相似度 max(assoc(A,A)+assoc(B,B))
assoc(A,A)=∑i∈A,j∈Awij
A类内相连边的权重
Ncut(A,B)=assoc(A,V)cut(A,B)+assoc(B,V)cut(A,B)
要使类间相似度最小,也就是分子最小
要使类内相似度最大,也就是(分母-分子)越大
目标 minNcut(A,B)
开始化简
cut(A,B)=assoc(A,V)−assoc(A,A)=assoc(B,V)−assoc(B,B)
Ncut(A,B)=assoc(A,V)cut(A,B)+assoc(B,V)cut(A,B)
=assoc(A,V)assoc(A,V)−assoc(A,A)+assoc(B,V)assoc(B,V)−assoc(B,B)
=2−(assoc(A,V)assoc(A,A)+assoc(B,V)assoc(B,B))
=2−Nassoc(A,B) (Nassoc(A,B)跟Ncut很像)
为了化简,使用一些技巧
x∈{1,−1}n
ifi∈A,xi=1 elseifi∈B,xi=−1 即在A类,x=1; 在B类,x=-1
di=∑jwij 也就是与i相连边的权重之和
我们的目标函数就可以变成
Ncut(A,B)=assoc(A,V)cut(A,B)+assoc(B,V)cut(A,B)
=∑xi>0di∑xi>0,xj<0−wijxixj+∑xi<0di∑xi<0,xj>0−wijxixj
cut(A,B)在A类x为+1,B类为-1,要计算权重和也就变成了 ∑xi>0,xj<0−wijxixj
assoc(A,V)计算与A中的点相连的边的权重之和,在A中的点x=+1,他上面连的边的权重 ∑xi>0di
继续化简
先提出两个矩阵
W∈Rn×nformedbywij
D∈Rn×nformedbydi
W=⎣⎡0w21w31w120w32w13w230⎦⎤
D=⎣⎡d1000d2000d3⎦⎤
提出一个系数
k=∑idi∑xi>0di也就是与第i个点相连的边的顶点在A中的权重所占所有边权重的比例
推导
D−W=⎣⎡d1−w21−w31−w12d2−w32−w13−w23d3⎦⎤
(1−x)在A中x为0,在B中x为2
(1+x)在A中x为2,在B中x为0
1全为1的向量
先来证明
4∑xi>0di∑xi>0,xj<0−wijxixj=(1−x)T(D−W)(1+x)
[1−x11−x2⋯1−xn]⎣⎡d1−w21−w31−w12d2−w32−w13−w23d3⎦⎤⎣⎢⎢⎡1+x11+x2⋯1+xn⎦⎥⎥⎤
=[(1−x1)d1−(1−x2)w21−⋯−(1−xn)w31−(1−x1)w12+(1−x2)d2−(1−x3)W32−⋯−(1−xn)wn2⋯]⎣⎢⎢⎡1+x11+x2⋯1+xn⎦⎥⎥⎤
=(1−x12)d1−(1−x2)(1+x1)w21−(1−x3)(1+x1)w31−⋯+(x2part)+(⋯)+(xnpart)
首先可知的是
(1−xi2)=0,所以 di系数都是0,我们可以不考虑
然后 wij的系数是 (1−xi)(1+xj),要使系数不为0,则 xi=1,xj=−1,即i在A类,j在B类
这里,我们就基本上证明了
4∑xi>0di∑xi>0,xj<0−wijxixj=(1−x)T(D−W)(1+x)
再来证明 ∑xi>0di=k1TD1
1TD1=[11⋯1]⎣⎡d1000d2000d3⎦⎤⎣⎡11⋯⎦⎤=d1+d2+⋯+dn
4Ncut(A,B)=k1TD1(1−x)T(D−W)(1+x)+(1−k)1TD1(1+x)T(D−W)(1−x)
继续做化简
提出另一个系数 b=1−kk这也就是在 B中权重A中权重
4Ncut(A,B)=k1TD1(1+x)T(D−W)(1+x)+(1−k)1TD1(1−x)T(D−W)(1−x)=b1TD1[(1+x)−b(1−x)]T(D−W)[(1+x)−b(1−x)]
令 y=(1+x)−b(1−x)
yTD1=i=1∑n(((1+xi)−b(1−xi))di)=2xi>0∑di−2bxi<0∑di=0
yTDy=i=1∑n(((1+xi)−b(1−xi))2di)=xi>0∑4di+xi<0∑4b2di
∑xi>0di=b∑xi<0di (B中权重A中权重⋅B中权重=A中权重)
⇒yTDy=4b(∑xi<0di+b∑xi<0di)=4b1TD1
综上
xminNcut(x)=yminyTDyyT(D−W)y
s.t.y∈{2,−2b}n,yTD1=0
我们放宽对y的限制
yminyTDyyT(D−W)y,y∈Rn,yTD1=0
接下来讨论如何求解y
瑞丽商
RayleighQuotient
xmaxxTBxxTAx⇒xmaxxTAxs.t.xTBx=1
L(x)=xTAx+λ(xTBx−1)
xTAx=[∑i=1nxiAi1⋯]⎣⎢⎢⎡x1x2⋯xn⎦⎥⎥⎤
=s=1∑nxsi=1∑nxiAis
∂xj∂L(x)=i=1∑nxiAij+s=1∑nxsAjs
推论
f(x)=xTAx,则 ∂x∂f(x)=(A+AT)x
这样就可以推得
∂x∂L(x)=0⇒(A+AT)x+λ(B+BT)x=0
如果A和B是对称矩阵
Ax=kBx,k=−λ
回到原题的计算
即求 (D−W)y=λDy
D−1(D−W)y=λy
即求 D−1(D−W)的特征向量(舍弃最小的特征值)
插一个矩阵的求导
对于一个函数 f:Rm×n↦R 从一个m×n的矩阵映射到实数,我们定义f对于A的导数为
∇Af(A)=⎣⎢⎡∂A11∂f⋮∂Am1∂f⋯⋱⋯∂A1n∂f⋮∂Amn∂f⎦⎥⎤
举个例子
A=[A11A21A12A22]
函数 f:R2×2↦R为
f(A)=23A11+5A122+A21A22
可以得到
∇Af(A)=[23A2210A12A21]
整体聚类的步骤:
- 假设 y1,y2,⋯,yk∈Rn×k是最小的k个特征向量
- 令 Y=[y1,y2,⋯,yk]∈Rn×k
- 矩阵Y的行可以看作原始数据的k维表示
- 利用k-means算法
为什么可以用y来做特征进行k-means聚类呢
首先要问,求出来的y是什么?
yi是Ncut(A,B)取最小值时对应的一组特征向量,y与x之间存在关系,y=(1+x)−b(1−x),x代表的是每个点的类别,那么我们可以认为,每个y对应着Ncut(A,B)最小时的一种分类方式
我们得到了一个 n×k的矩阵Y
Y=⎣⎢⎡y11⋮y1ny21⋮y2n⋯⋮⋯yk1⋮ykn⎦⎥⎤
我们相当于对 p1=[y11y21⋯yk1]
p2=[y12y22⋯yk2]
pn=[y1ny2n⋯ykn]
这n个元素做聚类
pi的意义是在对应着第i个元素最佳的k种分类方式
对 pi做聚类,也就是找到最相似的 pi们聚到一起,也就是在k种分类方式中,把经常分到一组的聚到一起
分类问题
什么是分类问题
从有标签的数据集(训练集)中提取规律,并应用规律对无标签数据集(测试集)进行分类
衡量分类好坏的标准
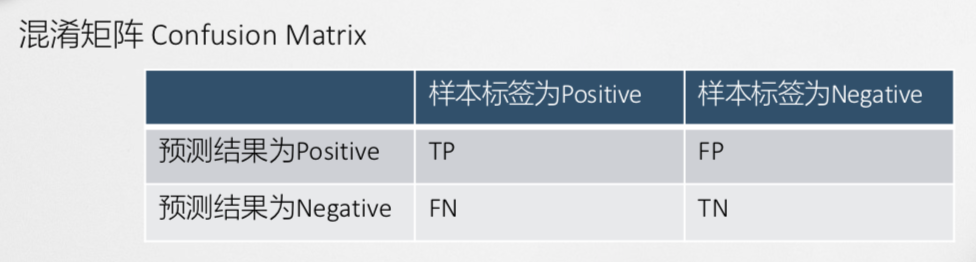
混淆矩阵
精确度
prercision=TP+FPTP
召回率
recall=TP+FNTP
F1score
F1=precision1+rercall12
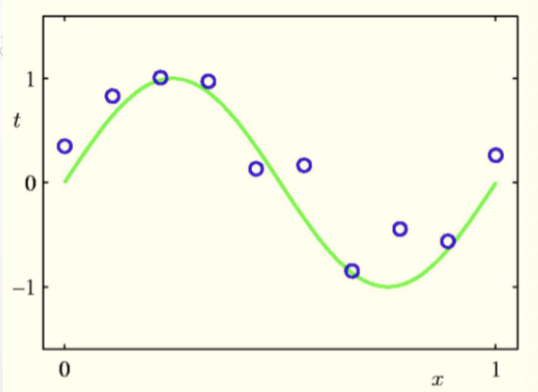
线性回归
曲线拟合
泰勒展开
h(x,θ)=θ0+θ1x+θ2x2+⋯+θnxn=i=0∑nθixi
x=[1,x,x2,⋯,xM]T
θ=[θ0,θ1,θ2,⋯,θn]T
h(x,θ)=θTx
分类问题中的线性回归
x∈A,h(x,θ)=0
x∈B,h(x,θ)=1
均方误差
MSE(θ)=21i=1∑n(yi−hθ(x(i)))2
目标函数
J(θ)=21i=1∑m(hθ(x(i))−y(i))2
目标是求$$J(\theta)=\frac{1}{2}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^2$$取最小值时的θ向量
迹
接下来介绍“迹”,“tr"。对于一个n×n的矩阵 A, A的迹是他对角线上的元素之和
trA=i=1∑nAii
迹的一些性质
trAB=trBA
假设A是m×n矩阵,B是n×m矩阵
A=⎣⎢⎡A11⋮Am1⋯⋱⋯A1n⋮Amn⎦⎥⎤
B=⎣⎢⎡B11⋮Bn1⋯⋱⋯B1m⋮Bnm⎦⎥⎤
AB=⎣⎢⎡A11⋮Am1⋯⋱⋯A1n⋮Amn⎦⎥⎤⎣⎢⎡B11⋮Bn1⋯⋱⋯B1m⋮Bnm⎦⎥⎤
BA=⎣⎢⎡B11⋮Bn1⋯⋱⋯B1m⋮Bnm⎦⎥⎤⎣⎢⎡A11⋮Am1⋯⋱⋯A1n⋮Amn⎦⎥⎤
trAB=i=1∑i=nA1iBi1+⋯+i=1∑i=nAmiBim=j=1∑j=mi=1∑i=nAjiBij=i=1∑i=nj=1∑j=mBijAji
trBA=j=1∑j=mB1jAj1+⋯+j=1∑j=mBnjAjn=i=1∑i=nj=1∑j=mBijAji
得到
trAB=trBA
易证
- trA=trAT
- tr(A+B)=trA+trB
- traA=atrA
下面是迹微分的一些性质:∣A∣表示行列式
- ∇AtrAB=BT
- ∇ATf(A)=(∇Af(A))T
- ∇AtrABATC=CAB+CTABT
- ∇A∣A∣=∣A∣(A−1)T 非奇异矩阵
A=⎣⎢⎡A11⋮Am1⋯⋱⋯A1n⋮Amn⎦⎥⎤B=⎣⎢⎡B11⋮Bn1⋯⋱⋯B1m⋮Bnm⎦⎥⎤
trAB=j=1∑j=mi=1∑i=nAjiBij∇AtrAB=∇A(j=1∑j=mi=1∑i=nAjiBij)=(Bij)=BT
左边矩阵的元素aij=∂Aji∂f右边矩阵的元素bij=∂Aji∂f=aij
∇Atr(ABATC)=∇Atr(ABXC)∣X=AT+∇Atr(YBATC)∣Y=A链式法则求导
∇Atr(ABXC)∣X=AT=∇AA(BXC)=(BXC)T=CTABT性质1
∇Atr(YBATC)∣Y=A=∇A(CTABTYT)=∇Atr(ABTATCT)考虑方阵和迹的性质
∇Atr(A(BTATCT))=CAB性质1
令C_ij为代数余子式
∣A∣=A1jC1j+⋯+AnjCnj左边aij=∂Aij∂∣A∣=Cij
由此可得
A=⎣⎢⎡C11⋮Cn1⋯⋱⋯C1n⋮Cnn⎦⎥⎤
A−1=∣A∣1A∗=∣A∣1×⎣⎢⎡C11⋮C1n⋯⋱⋯Cn1⋮Cnn⎦⎥⎤
右边=∣A∣(A−1)T=⎣⎢⎡C11⋮Cn1⋯⋱⋯C1n⋮Cnn⎦⎥⎤
解释第一条
假设我们有一个矩阵B∈Rn×m
我们可以定义一个函数f:Rm×n↦R
f(A)=trAB
这样的定义是有意义的,因为如果A∈Rm×n,那么AB就是一个方阵,可以求迹,因此f确实从Rm×n映射到R
接下来,我们着手找到使J(θ)取到最小值的θ.可以从把J写成向量矩阵的形式开始
对于一个训练集,定义一个设计矩阵X
X=⎣⎢⎢⎢⎡−−−−−−(x(1))T(x(2))T⋮(x(m))T−−−−−−⎦⎥⎥⎥⎤
同样,y是包含了训练集目标值的m维向量
y=⎣⎢⎢⎢⎡y(1)y(2)⋮y(m)⎦⎥⎥⎥⎤
我们有hθ(x(i))=(x(i))Tθ,可以得到
Xθ−y=X=⎣⎢⎢⎢⎡(x(1))Tθ(x(2))Tθ⋮(x(m))Tθ⎦⎥⎥⎥⎤−⎣⎢⎢⎢⎡y(1)y(2)⋮y(m)⎦⎥⎥⎥⎤=⎣⎢⎡hθ(x(1))−y(1)⋮hθ(x(m))−y(m)⎦⎥⎤
对于一个向量z,有zTz=∑_iz_i2
J(θ)=21i=1∑m(hθ(x(i))−y(i))2=21(Xθ−y)T(Xθ−y)
为了得到J(θ)的最小值,对θ微分
用上面的性质2,3
∇ATf(A)=∇Af(A)T
∇AtrABATC=CAB+CTABT
可以得到
- ∇ATtrABATC=∇A(trABATC)T=BTATCT+BATC
计算得出
∇θJ(θ)=∇θ21(Xθ−y)T(Xθ−y)
=21∇θ(θTXTXθ−θTXTy−yTXθ+yTy)因为∇θJ(θ)是实数,实数的迹是他本身
=21∇θtr(θTXTXθ−θTXTy−yTXθ+yTy)
=21∇θ(trθTXTXθ−2tryTXθ)
=21(XTXθ+XTXθ−2XTy)利用性质5,AT=θ,B=BT=XTX,C=I
=XTXθ−XTy利用性质1
为了得到J(θ)的最小值,使∇θJ(θ)=0, 可以得到正规方程
XTXθ=XTy
θ=(XTX)−1XTy
SVM
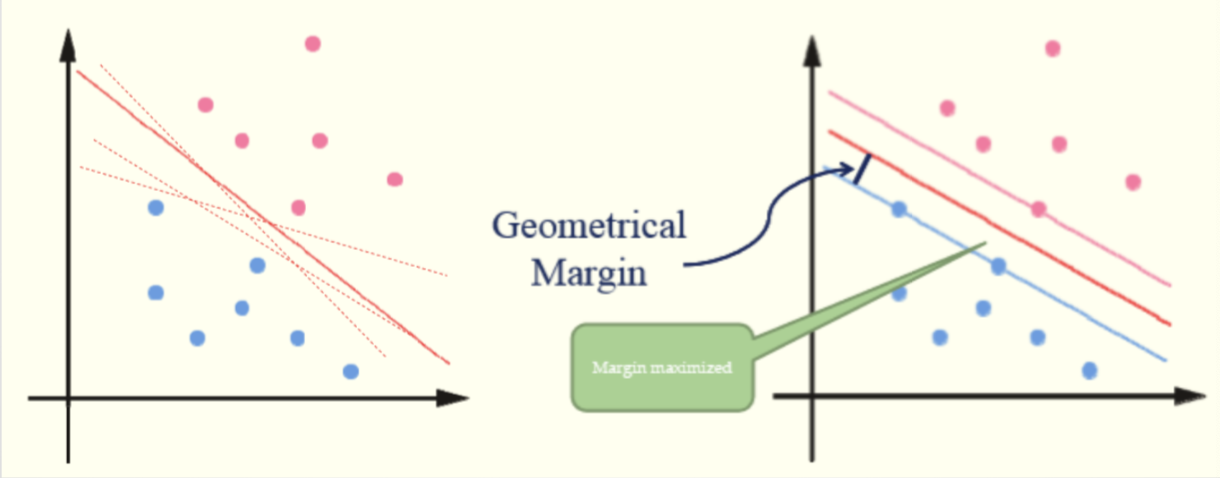
容易看到,这两种分类方法,第二种是更优的,我们可以认为在不同的分界线中,离数据点远点线是更优的
令我们需要拟合的直线为 wTx+b
函数间隔和几何间隔
给定一个训练样本 (x(i),y(i)),其中x是特征,y是结果 标签
定义函数间隔如下:
γ^(i)=y(i)(wTx(i)+b)
当y(i)=1时,γ^(i)应该hi是个大整数,y(i)=−1时 是个大负数
函数间隔越大,我们对分类结果越确信
定义全局样本上的函数间隔为
γ^=i=1,⋯,mminγ^(i)
定义几何间隔如下
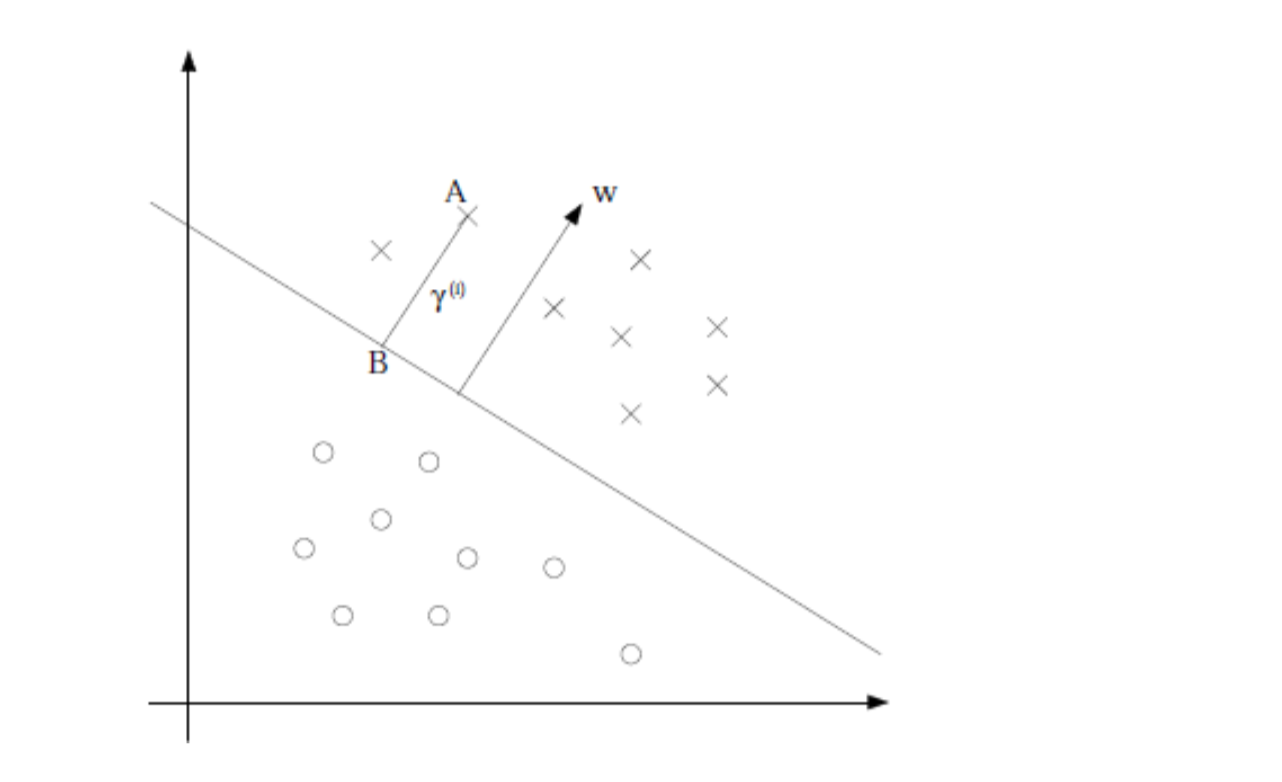
B在 wTx+b=0上,A到分割面的距离用 γ(i)表示,B是A在分割面上的投影
向量 BA的方向就是w的方向
这个地方产生了问题是因为没有想清楚 y=wTx+b如上图所示,两个坐标轴应该是 x1,x2,y是标圈和叉的那个维度,图为二维实则三维,所以是个分割面
A的坐标是 (x(i),y(i)),所以B的坐标应该是 x=x(i)−γ(i)∥w∥w(这里做的是向量减法)
带入 wTx+b=0
wT(x(i)−γ(i)∥w∥w)+b=0
解得γ(i)=∥w∥wTxi+b=(∥w∥w)Tx(i)+∥w∥b
通常,我们会将几何间隔定义为
γ(i)=y(i)(∥w∥w)Tx(i)+∥w∥b
我们可以看到 当∥w∥=1时,γ(i)=y(i)(wTx(i)+b)=y^,即几何间隔等于函数间隔
定义全局的几何间隔 γ=i=1,⋯,mminγ(i)
最优间隔分类器
我们要做的就是寻找一个分割面,使得离分割面最近的点和分割面的距离最大,距离越大我们就对一个样本分到正确的类越有信心
我们要使γ=i=1,⋯,mminγ(i)取到最大值,即
maxγ,w,bγs.t.y(i)(∥w∥w)Tx(i)+∥w∥b≥γi=1,⋯,m∥w∥=1
这里将 ∥w∥规约为1,因为几何间隔中 ∥w∥ 变成2,那么所有几何间隔缩小为原来的一半,对大小的比较不产生影响
但是 ∥w∥不是一个凸集,无法带入优化软件计算,我们考虑几何间隔与函数间隔 y^之间d 关系后得到
maxγ,w,b∥w∥γ^s.t.y(i)(wTx(i)+b)≥γ^i=1,⋯,m
这里的 w就不受∥w∥=1的限制了
但是目标函数依然不是凸函数,我们对 γ^做限制,取 γ^=1,那么离分割面最近的距离为 ∥w∥1,求 ∥w∥1的最大值相当于求 21∥w∥2的最小值,最后得到
minγ,w,b21∥w∥2s.t.y(i)(wTx(i)+b)≥1i=1,⋯,m
这是个二次规划问题,可以带入软件求解
补充凸优化
为什么要凸优化?
这种优化是一定可以找到全局最优的,因为不存在局部最优,只有一个最优点
所以对于梯度下降或其他的最优化算法而言,在非凸的情况下,很可能找到的只是个局部最优
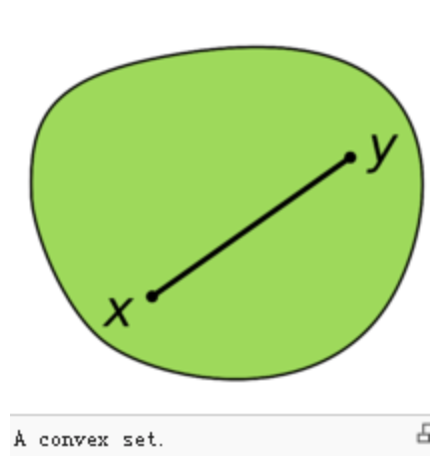
什么是凸集?
集合中任意两点的连线都在集合中
凸优化问题的定义
在凸集上寻找凸函数的全局最值的过程称为凸优化
即,目标函数(objective function)是凸函数,可行集(feasible set)为凸集
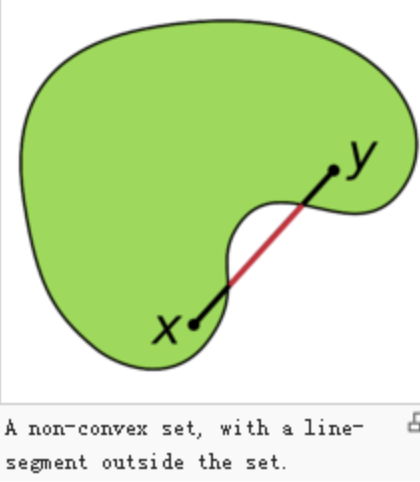
为何目标函数需要是凸函数?
这个比较容易理解,不是凸函数会有多个局部最优,如下图,不一定可以找到全局最优
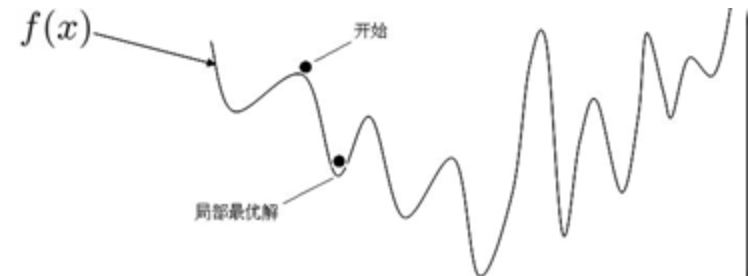
为何可行集需要为凸集?
稍微难理解一些,看下图
虽然目标函数为凸函数,但是如果可行集非凸集,一样无法找到全局最优
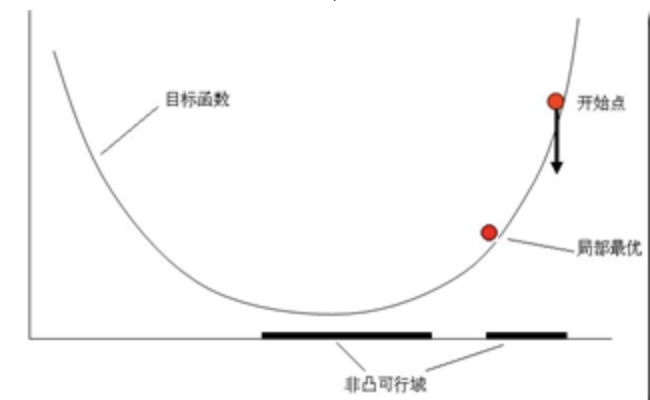
References:
[1] 吴恩达机器学习