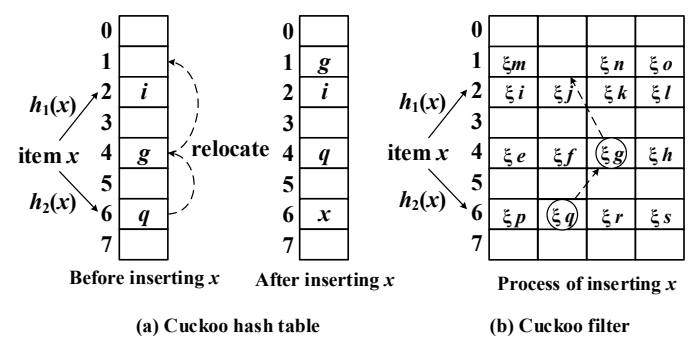
Bloom Filter
In computer science, a problem frequently occurs is determining whether an element belongs to a specific set (set membership test). A commonly used data structure is a hash table, which provides a fast and accurate search. However, a hash table could consume considerable space when there is a large amount of data.
Here comes a trade-off. If we lower our expectations for accuracy, can we achieve the goal to consume only a small space? In fact, in some scenarios, we don’t require 100% accuracy, maybe 80% or 90% accuracy is enough. Like the spider problem [4] proposed, a spider crawls the web and in the process, it needs to determine whether an URL has been crawled. 100% accuracy is not required, the cost of error is only crawling several websites that have been crawled.
Bloom Filter [5] can achieve this goal! A Bloom filter is a space-efficient probabilistic data structure [7].
Bloom Filter
Main components
-
an m-bit bit array
-
k hash functions
Operations
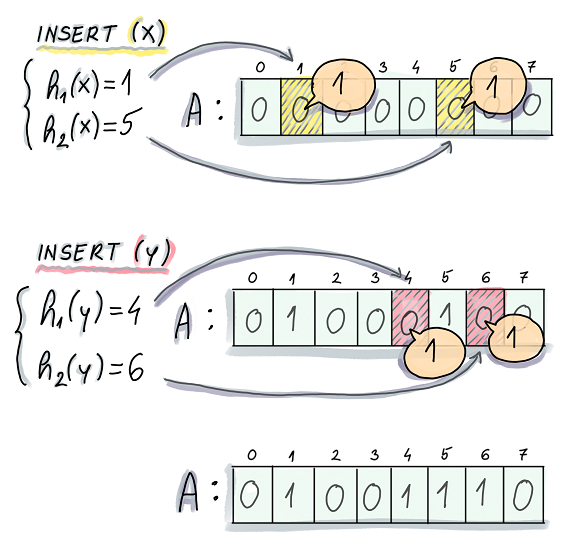
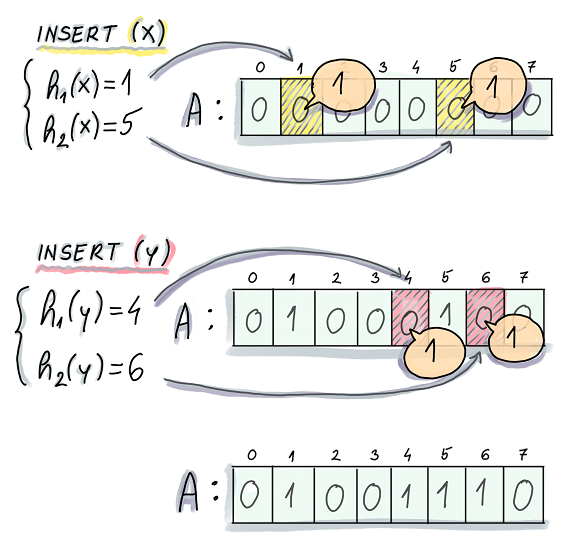
Insert
When inserting an element into the set, the element will be converted to k bits in the bit array by the k hash functions.
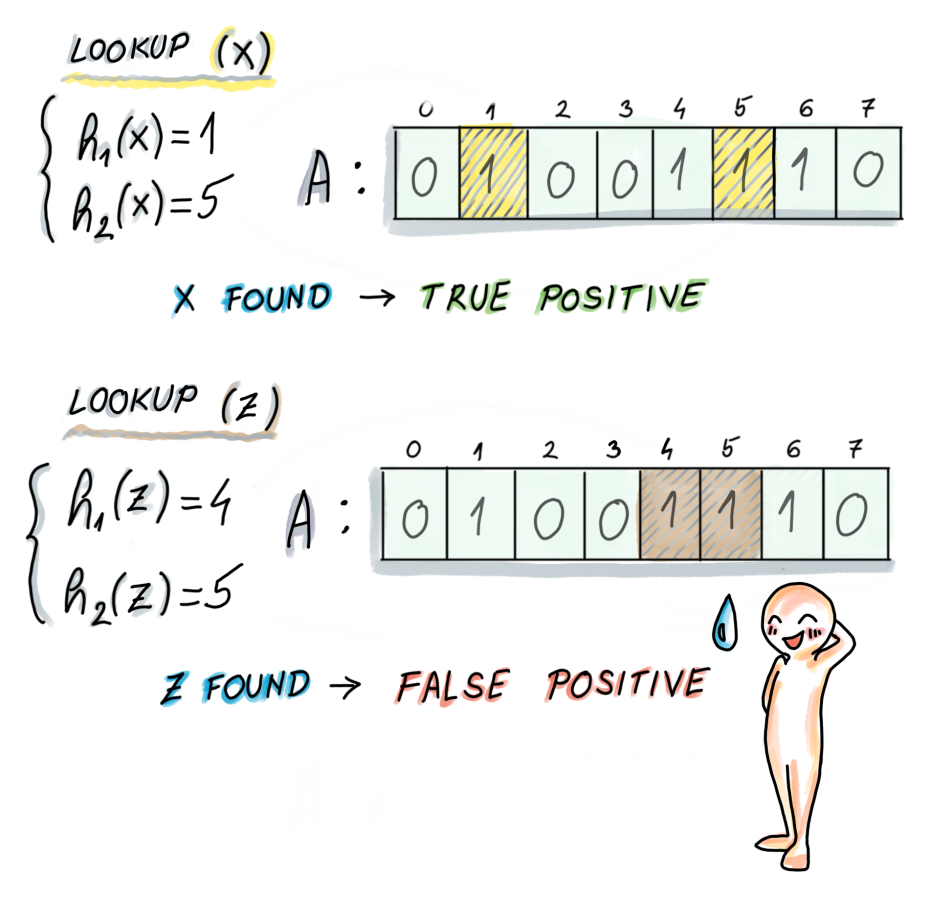
Lookup
When searching for an element, use the k bits produced by the k hash functions.
If one of the k bits in the bit array is 0, then the element can not be in the set.
If the k bits in the bit array are all 1, then the element may be in the set. (Because there might be some other elements hashed to the k bits --> false positive)
Deletion
is not supported, because deleting an element will influence the bits of other elements. If you want to delete an element, then the bit array must be reconstructed.
To do the deletion, the Counting bloom filter could be used.
Probability Analysis
The probability of false positives:
where n is the number of elements
The best m and k can be obtained from the probability function.
Variants
Counting Bloom Filter
CBF supports deletion.
structure: CBF uses an array of counters rather than bits.
operations:
-
insert: An insert increments the value of k counters instead of setting k bits.
-
lookup: A lookup checks if each of the required counters is non-zero
-
delete: A delete decrements the value of these k counters
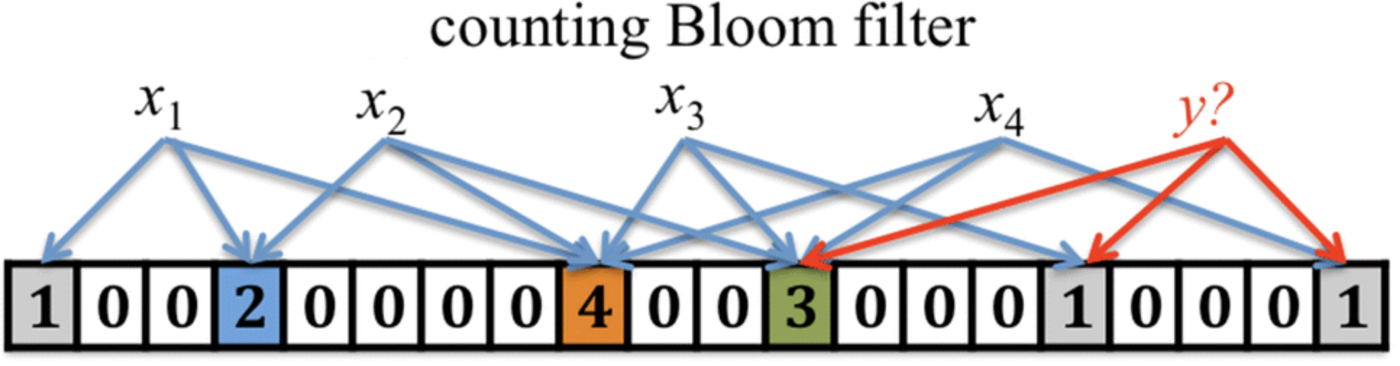
Note: Deletions will introduce the probability of false negatives during a query if the deleted input has not previously been inserted into the filter. Gou et al. provide heuristics for the parameters m, k, and n which minimize the probability of false negatives. [8]
Blocked Bloom Filter
BBF provides better spatial locality on lookups.
structure: A BBF consists of an array of small Bloom filters, each fitting in one CPU cache line.
d-left Counting Bloom Filters
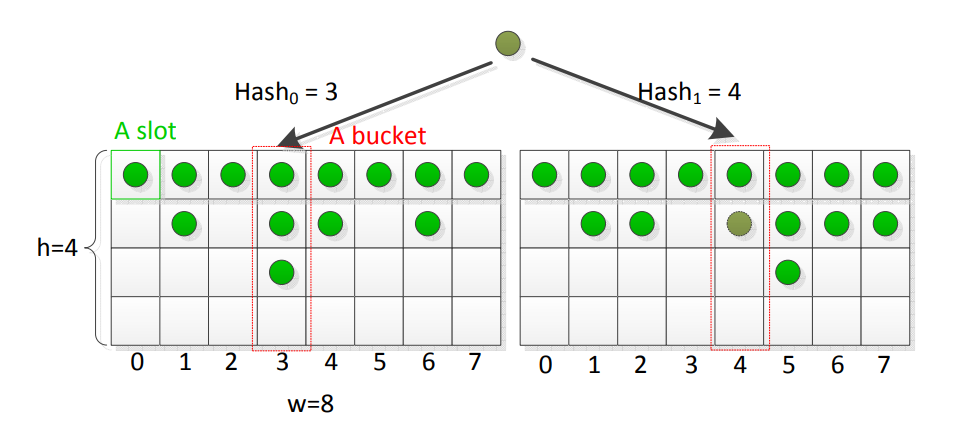
d-left hashing:
break the hash table into d equal sections (here d = 2); each section contains w buckets, each with h slots.
D-left hashing computes d hash functions on the input data and stores the data in the bucket with fewer items. In this figure, the value of the 2 hash functions is 3 and 4. Bucket 3 of the left section has 3 elements and Bucket 4 of the right section has only 1 element. So the element is inserted into the right section, bucket 4. [10]
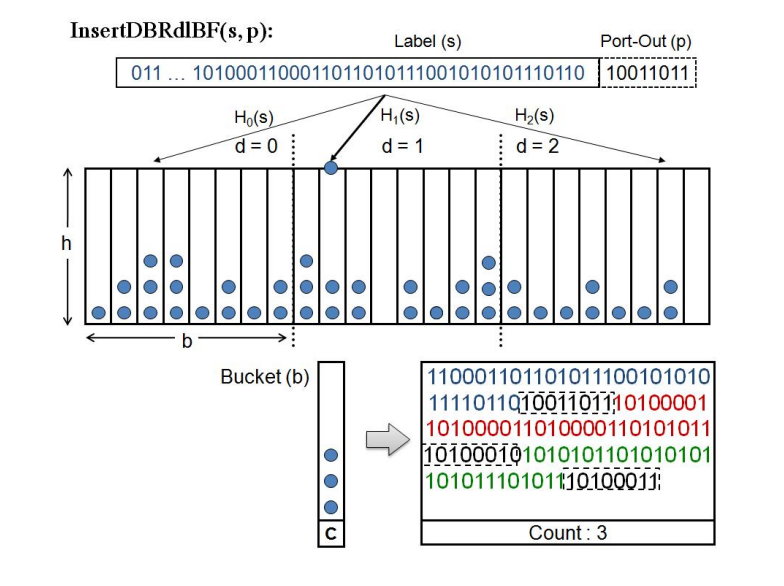
d-left Counting Bloom Filters
break the filter into d equal sections; each section contains w buckets, each with h slots. Every slot stores a counter and a fingerprint. [11]
Reference
[1] https://www.cs.jhu.edu/~langmea/resources/lecture_notes/115_bloom_filters_pub.pdf
[2] https://llimllib.github.io/bloomfilter-tutorial/
[3] https://zhuanlan.zhihu.com/p/306341095
[4] https://zhuanlan.zhihu.com/p/140545941
[5] Space/time trade-offs in hash coding with allowable errors
[6] https://freecontent.manning.com/all-about-bloom-filters/
[7] https://en.wikipedia.org/wiki/Bloom_filter
[8] https://en.wikipedia.org/wiki/Counting_Bloom_filter
[9] https://medium.com/analytics-vidhya/cbfs-44c66b1b4a78
[10] SAPTM: Towards High-Throughput Per-Flow Traffic Measurement with a Systolic Array-Like Architecture on FPGA
[11] Towards a new generation of information-oriented internetworking architectures